728x90

Given a m x n grid filled with non-negative numbers, find a path from top left to bottom right, which minimizes the sum of all numbers along its path.
Note: You can only move either down or right at any point in time.
Example 1:
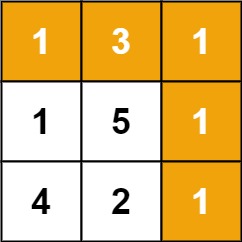
Input: grid = [[1,3,1],[1,5,1],[4,2,1]]
Output: 7
Explanation: Because the path 1 → 3 → 1 → 1 → 1 minimizes the sum.
Example 2:
Input: grid = [[1,2,3],[4,5,6]]
Output: 12
Constraints:
- m == grid.length
- n == grid[i].length
- 1 <= m, n <= 200
- 0 <= grid[i][j] <= 200
Code :
var minPathSum = function(grid) {
const m = grid.length; // 그리드의 행 수
const n = grid[0].length; // 그리드의 열 수
// 첫 번째 행을 누적합으로 업데이트
for (let i = 1; i < n; i++) {
grid[0][i] += grid[0][i - 1];
}
// 첫 번째 열을 누적합으로 업데이트
for (let i = 1; i < m; i++) {
grid[i][0] += grid[i - 1][0];
}
// 나머지 셀의 누적합 계산
for (let i = 1; i < m; i++) {
for (let j = 1; j < n; j++) {
grid[i][j] += Math.min(grid[i - 1][j], grid[i][j - 1]);
}
}
return grid[m - 1][n - 1]; // 우하단 셀의 최소 경로 합 반환
};
Solutions Code :
var minPathSum = function(grid) {
// 각 셀의 최소 경로 비용을 저장하는 그리드 생성
const minGrid = grid.map(row => row.map(_ => Infinity));
const m = grid.length - 1; // 그리드의 행 수
const n = grid[0].length - 1; // 그리드의 열 수
function getMin(x, y) {
let right = Infinity; // 오른쪽 이동의 비용
let down = Infinity; // 아래쪽 이동의 비용
// 도착 지점인 경우 현재 셀의 비용 반환
if (x === m && y === n) {
return grid[x][y];
}
// 이미 계산한 결과가 있는 경우 해당 값을 반환
if (minGrid[x][y] !== Infinity) {
return minGrid[x][y];
}
// 오른쪽으로 이동 가능한 경우
if (x !== m) {
right = getMin(x + 1, y);
}
// 아래쪽으로 이동 가능한 경우
if (y !== n) {
down = getMin(x, y + 1);
}
// 현재 위치의 최소 경로 비용 계산 및 저장
minGrid[x][y] = Math.min(right, down) + grid[x][y];
return minGrid[x][y];
}
// 시작 지점에서 우하단까지의 최소 경로 합 반환
return getMin(0, 0);
};
출처 : https://leetcode.com/problemset/all/
Problems - LeetCode
Boost your coding interview skills and confidence by practicing real interview questions with LeetCode. Our platform offers a range of essential problems for practice, as well as the latest questions being asked by top-tier companies.
leetcode.com
728x90
'LeetCode' 카테고리의 다른 글
| [LeetCode] 66. Plus One (2) | 2024.01.29 |
|---|---|
| [LeetCode] 65. Valid Number (2) | 2024.01.23 |
| [LeetCode] 63. Unique Paths II (0) | 2024.01.12 |
| [LeetCode] 62. Unique Paths (0) | 2024.01.12 |
| [LeetCode] 61. Rotate List (2) | 2024.01.09 |



